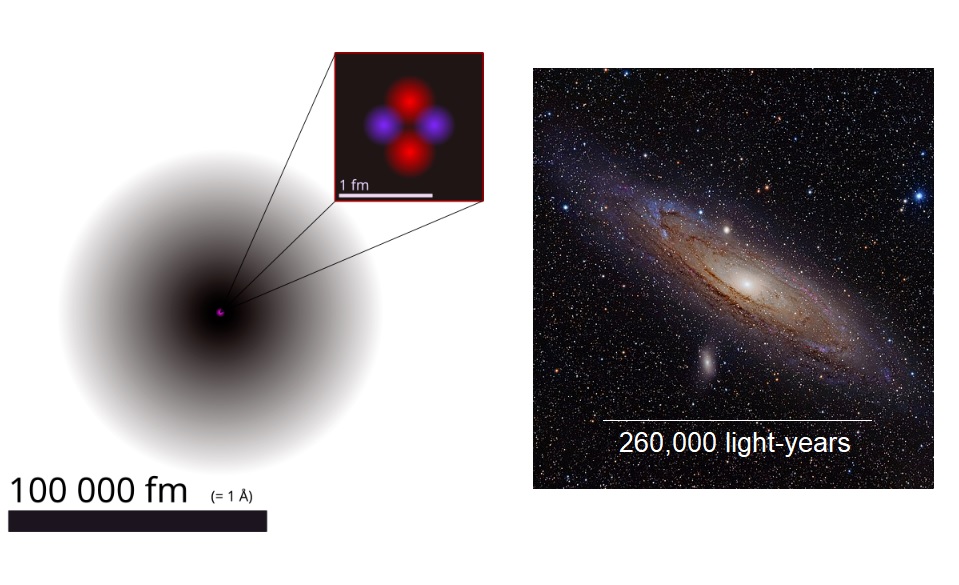
From about 10 years ago, a “new” type of questions seems to have become popular in the Singapore O and A level physics exams. These are questions on orders of magnitude. In simple English, this means “roughly how big”. And at about the same time, questions asking for specific numbers start to appear.
Browsing over the past 10 years of physics exam questions in school prelims, O and A level papers, I have seen questions that ask about the order of magnitude of the size of a phone, the speed of a person running, the size of the galaxy, diameter of Earth, diameter of an atom, diameter of its nucleus, wavelengths of colours of light, ...
“Order of magnitude” is not a phrase that is commonly used in everyday English. In fact, when I studied physics many years ago, I only first heard of it in the Cambridge university physics lectures. It was not taught in the Raffles Institution and Raffles Junior College physics classes that I attended.
And when I first, learnt about it in Cambridge, I found it really simple and useful for understanding physics. For example, very huge objects like Suns and galaxies can have very different physics from very small objects like atoms and electrons. But when I see it in recent years of O and A level physics papers, it gives a rather different feeling. Instead of understanding physics, the questions just want us to memorise specific examples. Like the size of Earth, and the diameter of an atom.
In simple English, “order of magnitude” just means “roughly how big something is”. Of course, being physics, it needs a bit more understanding. There are some simple rules or maths to go with it – using powers of 10.
For examples :
- The length of a running track would be the order of magnitude 102 m ~ 100 m.
- The mass of an adult would be the order of magnitude 102 kg ~ 100 kg.
- The size of a bacteria 10-6 m ~ 1 μm.
- Radius of Earth 107 m ~ 10000 km (more accurately 6400 km)
To put it in a simple way – in physics, if we want to roughly say how big something is, we try to use the closest power of 10. This is called “order of magnitude”,
For example, the order of magnitude of the height of a person is 1 m. But this may not sound right to most people, who would naturally think of the height of an adult as closer to 2 m. So it does take some getting used to. The purpose of using it is not to tell the difference between one person and another person. It is more for telling apart two very different sizes – like a person and a dinosaur. Or a football and an atom.
Order of Magnitude in Physics: Understanding the Scale of Physical Quantities
In physics, the concept of order of magnitude is a powerful tool that helps scientists and engineers comprehend and compare the sizes of different physical quantities. It is often used to describe the scale of numbers, from incredibly small to immensely large, in a way that is easy to understand, without getting lost in the complexity of exact values. The idea of order of magnitude allows us to make quick approximations, simplify calculations, and grasp the relative significance of different phenomena.
This article delves into the concept of order of magnitude in physics, exploring its definition, application, and importance in scientific reasoning and problem-solving. We will examine how order of magnitude is determined, its relevance in various fields of physics, and the role it plays in making sense of the universe around us.
1. What is Order of Magnitude?
The term "order of magnitude" refers to the scale or size of a physical quantity in powers of ten. It provides a way to express the approximate size of a value in a form that is more manageable and easy to compare. In simple terms, it gives a rough estimate of how large or small a number is by rounding it to the nearest power of 10.
For example, if a quantity is of the order of magnitude of 103, it means that the quantity is on the scale of 1,000. Similarly, if a quantity is of the order of magnitude of 10−6, it means the quantity is in the range of 0.000001.
Order of magnitude is commonly used in scientific notation, which allows us to express very large or very small numbers more conveniently. Instead of writing out long strings of zeros, scientists can use exponents to convey the scale of a number.
2. Why is Order of Magnitude Important?
Order of magnitude is significant in both theoretical and experimental physics for several reasons:
a. Simplifying Complex Numbers
Many quantities in physics can vary across multiple orders of magnitude, making it difficult to express or compare them directly. For instance, in the study of astrophysics, the mass of a planet like Jupiter is roughly 1027 kilograms, while the mass of an electron is around 10−31 kilograms. The vast difference in these numbers can be overwhelming if we try to work with the exact values at all times. By using orders of magnitude, physicists can focus on the relative sizes of these quantities and neglect the smaller, less significant digits.
b. Comparing Quantities
By expressing values in terms of orders of magnitude, scientists can more easily compare different physical phenomena. For instance, when comparing the energy output of the Sun to that of a light bulb, it's much more intuitive to think in terms of orders of magnitude, even though the actual numbers differ by several powers of ten. This comparison helps researchers gauge the importance or scale of different effects in nature.
c. Estimating and Approximating
When performing calculations in physics, it's often useful to estimate values to the nearest order of magnitude instead of trying to obtain exact figures. This simplification allows for quicker approximations, which are particularly valuable in situations where time or computational resources are limited. In many cases, an order of magnitude estimate can provide enough accuracy for practical purposes, especially when dealing with very large or small quantities.
3. How is Order of Magnitude Determined?
To determine the order of magnitude of a number, the goal is to express it as a power of 10. There are different methods for doing this, depending on the nature of the number (whether it's large, small, or in between). Here's how we can generally determine the order of magnitude:
a. Large Numbers
For large numbers, we express the quantity in scientific notation, where the number is written as a product of a coefficient (between 1 and 10) and a power of 10. The exponent of 10 in the scientific notation gives the order of magnitude.
For example:
• The number 3,000 can be written as 3×103 , so its order of magnitude is 103.
• The number 2,500,000 can be written as 2.5×106, so its order of magnitude is 106.
b. Small Numbers
For small numbers, we use negative exponents of 10 in scientific notation. These negative exponents correspond to orders of magnitude that are less than 1.
For example:
• The number 0.000007 can be written as 7×10−6, so its order of magnitude is 10−6.
• The number 0.00000032 can be written as 3.2×10−7, so its order of magnitude is 10−7.
c. Rounding to the Nearest Power of Ten
In many cases, the order of magnitude is found by rounding a number to the nearest power of ten. If the number is exactly halfway between two powers of ten, we typically round to the higher one. This approximation makes it easier to compare values and assess their scale.
4. Applications of Order of Magnitude in Physics
Order of magnitude plays a crucial role in many areas of physics, especially when dealing with quantities that span a wide range. Here are some examples of how this concept is used:
a. Astronomy and Cosmology
In astronomy, the scales of distances, masses, and times can be mind-bogglingly large. For example, the distance from the Earth to the Sun is approximately 1.496×108 kilometers, and the mass of the Sun is roughly 2×1030 kilograms. These numbers are so large that it's much easier to discuss them in terms of their order of magnitude, such as 108 kilometers and 1030 kilograms. Similarly, the size of the observable universe is on the order of 1026 meters, and the age of the universe is about 1010 years. By expressing these vast numbers in terms of orders of magnitude, astronomers can better understand and communicate the scale of the universe.
b. Particle Physics
At the other end of the scale, particle physics deals with incredibly small quantities. For example, the size of an atomic nucleus is on the order of 10−15 meters, while the Planck length (the smallest meaningful length in quantum gravity) is on the order of 10−35 meters. By working with these orders of magnitude, physicists can conceptualize the minuscule scales involved in subatomic phenomena.
c. Classical Mechanics and Engineering
In classical mechanics, the forces acting on objects can vary widely. The weight of an apple, for instance, is on the order of 101 newtons (about 10 N), while the gravitational force between the Earth and the Moon is on the order of 1020 newtons. In engineering, order of magnitude estimates are often used to assess the feasibility of different designs or systems, especially when working with large or small machines and devices.
d. Thermodynamics and Heat Transfer
In thermodynamics, the energy of different systems can differ by many orders of magnitude. For example, the energy content of a single molecule of water is on the order of 10−21 joules, while the energy produced by burning a kilogram of coal can be on the order of 107 joules. Understanding the order of magnitude of these energies helps engineers design systems for power generation, heating, and cooling.
5. Limitations and Considerations
While the order of magnitude is a valuable concept, there are some limitations and considerations when using it:
a. Loss of Precision
By rounding numbers to their orders of magnitude, we sacrifice some precision. This is acceptable in many cases, especially when the goal is to obtain an approximate understanding of the size or scale of a quantity. However, in situations where accuracy is crucial, such as in certain experimental measurements, the exact value may be necessary.
b. Context-Specific Estimates
The order of magnitude provides a rough estimate but may not fully capture the subtleties of a particular situation. In some contexts, a more detailed analysis may be required, particularly when dealing with phenomena that span multiple orders of magnitude, as is often the case in cosmology or quantum mechanics.
Conclusion
The concept of order of magnitude is a fundamental tool in physics, enabling scientists and engineers to understand and compare quantities that vary across vast scales. Whether working with the massive distances in astronomy or the tiny particles in quantum mechanics, order of magnitude provides a means of simplifying calculations, making approximations, and gaining insight into the physical world. By focusing on the powers of ten, physicists can quickly assess the relative importance of different quantities, identify patterns, and solve problems more efficiently. This concept plays a critical role in helping us grasp the enormity of the universe, as well as the intricacies of the microscopic world.
You can learn these concepts and more at Dr Hock's maths and physics tuition.